Shannon-Fano-Elias coding and Arithmetic Coding

Shanon-Fano-Elias coding

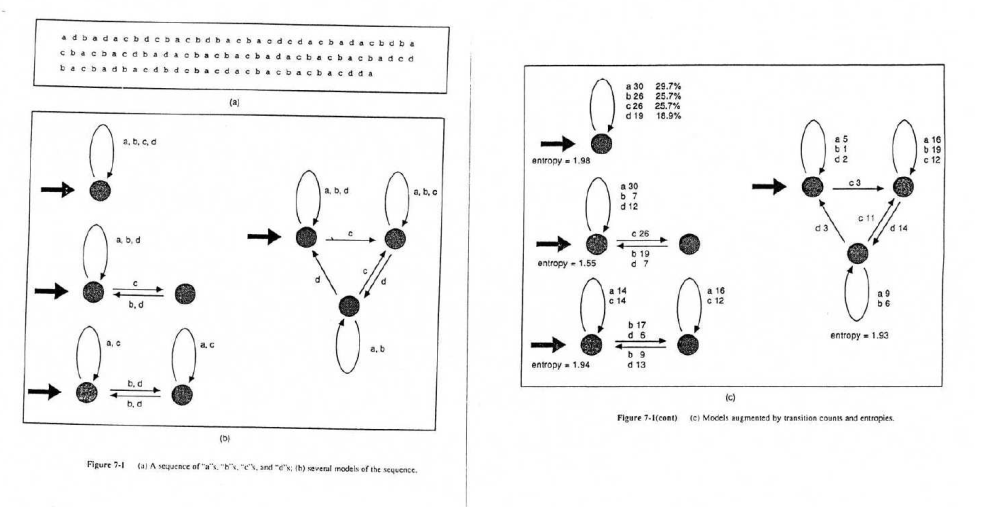
Knowing the symbols probabilities, SFE codes a truncated binary representation the cumulative distribution function. (and not proba directly because can have same value).

Probabilities for symbols are: $P(X=a_i) = p(a_i)$
Cumulative distribution function $F(x) = \sum_{i \leqslant x}p(a_i)$
We can introduce:

$$\tilde{F}(a_i) = \sum_{k}^{i-1}p(a_k) + \frac{p(a_i)}{2}$$

It corresponds to the middle point of a step in the distribition plot.
For a given $\tilde{F}(a_i)$, it is possible to retrieve $a_i$. (see figure)
We use this value because it’s also possible to retieve $a_i$ with an approximation of $\tilde{F}$.

What precision do we need to retrieve $a_i$?

Let’s truncate by $l_i$ bits (denoted by ${\lfloor \tilde{F}(i) \rfloor}_{l_i}$)
Then by definition of truncation to $l_i$ bits:

$$\overbrace{\tilde{F}(i) - {\lfloor \tilde{F}(i) \rfloor}_{l_i}}^{Fractional\_part} < \frac{1}{2^{l_i}}$$

Lets chose $l_i = \lceil -log(p(i)) \rceil + 1$
Then:

$$2^{-l_i} = 2^{- \lceil - log(p(i)) \rceil - 1} \leqslant 2^{log(p(i)) - 1} = \frac{p(i)}{2} = \tilde{F}(i) - F(i-1)$$ $$\implies {\lfloor \tilde{F}(i) \rfloor}_{l_i} > F(i-1)$$

Hence this value of $l_i$ ensures ${\lfloor \tilde{F}(i) \rfloor}_{l_i} \in \left]F(i-1), \tilde{F}(i)\right]$

Is this code of prefix?

Let the codeword $b_1b_2...b_l$ represent $[0.b_1b_2...b_l, 0.b_1b_2...b_l + \frac{1}{2^l}]$
Any number outside this interval has at least a bit between 1 and $l$ that changes –> not a prefix of a codeword of another interval.

In the case of the SFE, all intervals are separated (see figure) so it is prefix.

Example

Performance

Codeword length:

$$L = {\sum}{p(i)l_i} = \sum{p(i)*(\lceil -log(p(i)) \rceil + 1)} < H + 2$$

The performance can be improved by coding several symbols in each codeword.
This leads to arithmetic coding.

Arithmetic coding

Principle

Arithmetic coding is a generalization of the SFE.
Its aim is to code a sequence $x^n = x_1x_2...x_n$ on the fly knowing the probabilities of the symbols.
Let $F(x^n)$ be the cumulative probabilty distribution. We want to compute it at each step, in order to finally have the unique: $[ F(x^n)-p(x_n) , F(x^n)]$
The final codeword will be in this interval.

The principle to determining the interval is the following:

• divide the interval proportionally to the primary cumulative distribution, to each interval its corresponding symbol is associated.
• chose subinterval of symbol to be coded. This new interval is itself divided in subinterval with respect to the primary probability distribution.
• proceed until the sequence is over.

Total probability: $p(x^n)$ = product of probabilities of each character = is the size of the interval.
Hence at the end the codeword is: ${\lfloor \tilde{F}(x^n) \rfloor}_{l(x^n)}$
with: $l(x^n) = \lceil -log(p(x^n)) \rceil + 1$

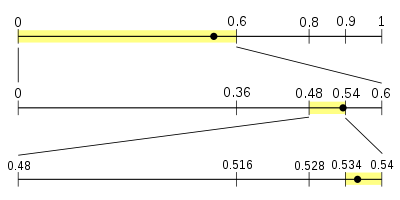
Remark: in order to decode, only need to follow the path given by the intervals to find value.

Benefits

Huffman can only come close to $H$ by using large block of code. Which means you need a pre-designed codebook of exponentially growing size (huffmantree).
On the opposite, AC enables coding large blocks w/o having to know codewords a priori –> generate code for entire sequence directly.
Furthermore it has the ability to be adaptable.

Adaptative models for arithmetic coding

During the processing of a sequence, given the information we already have, we can use predictive models to define the probability of the current symbol.

Example for text:

Given the previous seen text, we can find the probality for a symbol to be the next letter:

$$. \to space$$

Type of models

According to flexibility

• static
• semistatic
• adaptive

According to quantity of preceding text taken into account

• finite context model of order $m$: m previous symbols used to make prediction (size of the word).
  For instance, prediction by partial matching (PPM) uses finite context models, for each symbol, context starts at n:
  • decrease order:
    • if unseen context: decrease
    • if seen context but unseen encoded char after it: escape symbol
    • else: use probability Finally the char will have all the escapes probs + prob of char.
      If no context for this char use simple model of equiprobabilty.

• finite state models: the probabilities are obtained by modelling the best finite state machines representing the sequence. Each transition has a probability associated with it.